
1. Chain and Offset:
Distances along a line are measured to points at right angles to the feature to be mapped. The offset distance (or perpendicular distance) is then measured to the feature. The data acquired is not usually computed but plotted directly (allowing for chainage corrections).

2. Distance/Distance Intersection:
Two distances from either end of a base line are measured to the feature to be mapped. The distances can be plotted directly to scale, or can be reduced to coordinates using the fundamental triangle formulae.
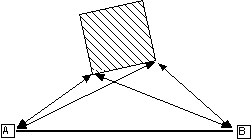
3. Angle/Angle Intersection:
Two angles are measured from either end of a known baseline to the feature to be mapped. Again, the angles can be plotted directly or reduced to coordinate values using the sine and/or cosine formulae. The angles can also be reduced to coordinates by the intersection formula:
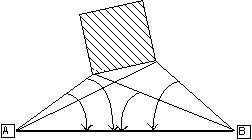
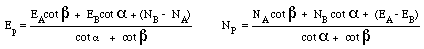
4. Radiation:
A directionand a distance are measured
from a known point to the feature to be mapped. The data can be plotted
directly to scale, or can be reduced to coordinates using the formulae
below where theta is a bearing:

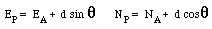
5. Resection:
This method is a little different in that the stand point is unknown, and three directions are measured to three known features. Commonly used by bushwalkers for position fixing, but also capable of high accuracy when appropriate equipment is used. Reduced using fundamental triangle geometry, or more easily with Tienstra's formula:
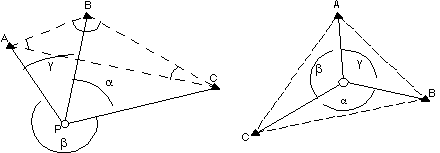
Watch how the angles are named when changing the geometry of the field observations. Alpha, beta and gamma are observed, A B and C are obtained from the coordinates of the known points.
The full derivation of this can be found in Bannister, Raymond and Baker, Surveying 6th Edition, p190.