Es sei der reelle 4-dimensionale Vektorraum
gegeben, auf dem das Minkowski-Skalarprodukt (nach H. Minkowski aus Kaunas in Litauen (1864 - 1909))
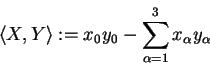
für ![]() definiert ist. Das Paar
definiert ist. Das Paar ![]() heißt Minkowski-Raum, die Konstante c > 0 Lichtgeschwindigkeit.
Ein Vektor
heißt Minkowski-Raum, die Konstante c > 0 Lichtgeschwindigkeit.
Ein Vektor ![]() heißt zeitartig, wenn
heißt zeitartig, wenn ![]() ,
raumartig, wenn
,
raumartig, wenn ![]() ist, und lichtartig wenn
ist, und lichtartig wenn ![]() ist.
ist.
Die Lichtgeschwindigkeit c wird benutzt (etwa in ![]() ),
damit man statt der Zeitachse
),
damit man statt der Zeitachse ![]() mit der Dimension [sec] die Koordinatenachse
mit der Dimension [sec] die Koordinatenachse ![]() mit der Dimension [m] bekommt.
mit der Dimension [m] bekommt.
Die zeitartigen Vektoren von ![]() bilden einen Kegel
bilden einen Kegel ![]() mit dem Rand
mit dem Rand ![]() ,
,
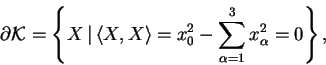
dem Lichtkegel:
![\begin{picture}(83.00,49.00)%\vector(62.67,9.00)(62.67,49.00)\put(62.67,49.0......,0)[cc]{$x_{1}$ }}\put(83.00,34.33){\makebox(0,0)[cc]{$x_{2}$ }}\end{picture}](img43.gif)
Ein zeitartiger Vektor X heißt zukunftgerichtet, wenn x0 > 0.
Ein zukunftgerichteter zeitartiger Vektor
stellt den 4er-Geschwindigkeitsvektor eines Punktes dar, der im Newtonschen Bild durch
dargestellt wird, und es gilt für den Betrag von ![]() ,
also für
,
also für ![]() dann:
dann:
d. h. ein zeitartiger Vektor repräsentiert den 3-dimensionalen
Newtonschen
Geschwindigkeitsvektor ![]() eines Punktes, der sich langsamer als das Licht bewegt. Die Größe
eines Punktes, der sich langsamer als das Licht bewegt. Die Größe ![]() heißt Eigenzeit (,,erlebte Zeit'') eines Teilchens, das sich
entlang X bewegt. Wenn X raumartig ist, ist
heißt Eigenzeit (,,erlebte Zeit'') eines Teilchens, das sich
entlang X bewegt. Wenn X raumartig ist, ist ![]() imaginär und so nicht erklärt. Ein Teilchen, das sich mit Lichtgeschwindigkeit
bewegt, ein Photon, für das also
imaginär und so nicht erklärt. Ein Teilchen, das sich mit Lichtgeschwindigkeit
bewegt, ein Photon, für das also ![]() gilt, wird dargestellt durch einen lichtartigen Vektor X mit
gilt, wird dargestellt durch einen lichtartigen Vektor X mit ![]() ;
ein solches Teilchen erlebt also keine Eigenzeit. Deshalb ist so die Lichtgeschwindigkeit
auch ,,Grenzgeschwindigkeit''.
;
ein solches Teilchen erlebt also keine Eigenzeit. Deshalb ist so die Lichtgeschwindigkeit
auch ,,Grenzgeschwindigkeit''.
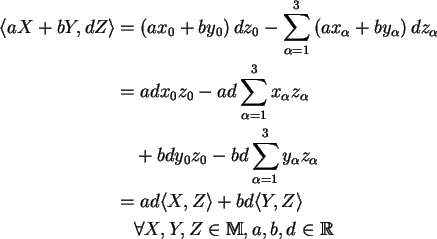
Mit (i) folgt die Bilinearität.
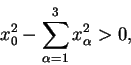
und da X zukunftgerichtet ist, gilt
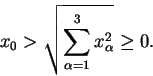
Analog für Y. Wegen der Cauchy-Schwarz'schen Ungleichung ist
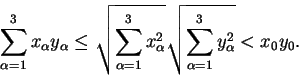
Also gilt
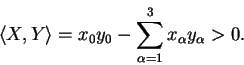
Damit können wir das Zwillings-,,paradoxon'' erklären. Denn es gilt:
Für zwei nichtverschwindende, zeitartige und zukunftgerichtete Vektoren ist immer
und wenn zusätzlich X und Y nicht parallel sind, gilt auch:
also die umgekehrte Dreiecksungleichung (wrong-way triangle inequality).
![\begin{picture}(69.00,50.00)%\vector(44.33,10.00)(44.33,50.00)\put(44.33,50.......ox(0,0)[cc]{$X$ }}\put(40.67,32.00){\makebox(0,0)[rc]{$X + Y$ }}\end{picture}](img66.gif)
Ist aber W := X + Y,
kann man für W ein ,,mitbewegtes'' Koordinatensystem einführen,
in welchem ![]() ist.
ist.
Dann ist in diesem Koordinatensystem natürlich
und
und ![]() ,
damit X + Y = W ist.
,
damit X + Y = W ist.
Dann ist
und
so daß gilt
Also ist
und
falls ![]() oder X und Y nicht parallel sind.
oder X und Y nicht parallel sind.
Man beachte, daß die zulässigen Koordinatenwechsel in ![]() die Minkowski-Längen
die Minkowski-Längen ![]() als die Quadrate der Eigenzeit
als die Quadrate der Eigenzeit ![]() invariant lassen, auch wenn die Koordinaten X
= (x0, x1, x2, x3)
sich ändern können.
invariant lassen, auch wenn die Koordinaten X
= (x0, x1, x2, x3)
sich ändern können.
Die Eigenzeit entlang W = X + Y ist also länger
als die entlang X und danach entlang Y.
Mit anderen Worten:
| Der Zwilling, der sich entlang dem (scheinbar kürzeren) Vektor X + Y bewegt, wird älter als der, der sich entlang X und dann entlang Y bewegt. |
Natürlich braucht dieser aber einmal viel Energie, um die Geschwindigkeit X in die Y zu ändern; er muß mit Masse M auch seinen Impuls ändern.
Next:Allgemeine RelativitätstheorieUp:Ringvorlesung ,,Geschichte der Mathematik'' Previous:Zur Geschichte des Kalenders